

|
Micscape Snippets 1 - On soccer balls, insect compound eyes ...... and Euler
by David Walker, UK
|
Series Introduction: Occasional random jottings by the Micscape Ed.
Mother Nature's clever use of geometry, from the simplest to the most intricate forms never ceases to amaze. There's a wide variety of examples to attract the attention of even the casual observer—whether it is the spirals of snails, the symmetry of starfish or the fractal type forms of fern leaves. But for the microscopy enthusiast, her use of complex 3D geometry becomes particularly striking in forms such as diatom frustules and radiolaria shells.
Nature's use of hexagonal facets in the compound eyes of many insects is an example where a simple geometric form is used to great effect. Removing and clearing the whole eye of a dead insect or removing just the cornea to make a permanent mount are popular subjects to study under the microscope.
In the October 2012 issue of Micscape I shared a project to study the compound eye of the cultivated silk moth Bombyx mori. I was intrigued by Leeuwenhoek's study reported in his letter dated April 20th 1702 to Karl, Landgrave of Hessen-Kassel where he manipulated the eye of this moth under his single lens microscope to estimate the total number of facets. Attempting a comparable study using both a stereo microscope and with a modern replica of his single lens microscope provided a hands-on insight into his dexterity and visual acuity. Some images from this project are shared below.



Above: The cultivated silk moth female Bombyx mori, head, whole eye and cleared eye. The eye along its widest diameter is ca. 1.4 mm.
To calculate the number of facets from measurements under the microscope, some thought has to be given to the geometry of tiling a sphere with hexagons, the idealised form of the compound eye. Leeuwenhoek described his approach to do this and the method was improved by a later worker Gorham in 1853. Hexagons alone can perfectly 'tile' a flat surface leaving no gaps (e.g. the honey bees' wax honeycomb) but hexagons are unable to perfectly tile the surface of a sphere. A familiar example of this is the typical modern soccer ball. It is a truncated icosahedron—20 hexagons partially tile the sphere but also requires 12 pentagons to completely tile.

Above: An illustration that hexagons alone cannot tile a sphere. A truncated icosahedron (Wikipedia entry) compared with its spherical form as used in many soccer balls. Image used under the Wikipedia Creative Commons Licence, image credited to Aaron Rotenberg with thanks.
This made me wonder about the geometry associated with hexagonal tiling of a sphere as each tile become progressively smaller with respect to the sphere diameter. As the hexagons become very small, as with the insect compound eye, the surface area occupied by each hexagon occupies becomes flatter—does this imply (using my admittedly naive grasp of maths) that at the limit of using the tiniest facets that complete tiling is possible with hexagons alone?
I didn't explore this aspect further at the time but recently sought some insight on the maths of tiling spheres with hexagons at the Mathematics Stack Exchange. The Stack Exchange group of forums are more rigorous than most with questions being voted up or down by members which build up a user's 'reputation', or even blocked if not regarded as up to scratch. Fortunately the question passed muster and I received some helpful replies. In particular I am indebted to forum member Ross Millikan who gave a very clear and definitive answer in a few lines using some simple but elegant maths by one of the greatest mathematicians of all time, Leonhard Euler.
Euler's Polyhedron Formula V - E + F = 2 (where V, E and F are the number of vertices, edges and faces) applies to spherical polyhedra and can be used to provide an exact answer as to how many pentagons are required to 'fill' the spaces on a sphere tiled with hexagons as the face size decreases. See Ross Millikan's answer for the simple work through but the answer is 12, exactly the same as the soccer ball—the size and thus number of hexagons plays no part.
Maybe I'm easily pleased with any interesting insight linking the microscopic world of Nature to pure science or maths, but the simple elegance of the approach to the solution both delighted and intrigued me. If Mother Nature created an idealised hexagonal tiling of a perfect hemisphere for each compound insect eye, there should be just 12 pentagons for both eyes intermingled with the hexagonal facets. The estimated total number of facets for both silk moth eyes combined was 6236 by Leeuwenhoek and mine was 7233 with the Gorham correction, see Micscape article).
In reality, Nature may have workarounds to tile the eye with hexagons—the eye may not be a perfect part of a sphere, or has some distorted/asymmetric hexagons and/or uses various polygons to complete the sphere. (Each silk moth eye in my study was ca. 2/3rds of a hemisphere). The cleared cornea I studied of the silk moth is shown below. Some folding and distorting of the cornea during preparation may skew any study, but in the better mounted areas, there's perfect hexagonal packing and the occasional perfect pentagonal facet, a selection shown in yellow. Although there's more pentagons than required for the idealised part sphere.
For someone with a lot of time on their hands and good manipulation skills, it would be interesting to study a selection of whole undistorted insect eyes of different species mounted on a 3D spindle stage to see how Nature works around the inability to tile part of a sphere with hexagonal facets only. Does Nature solely use pentagons as 'fillers' or also other techniques—if just pentagons, how close does Euler's prediction apply of only 12 pentagons being present?
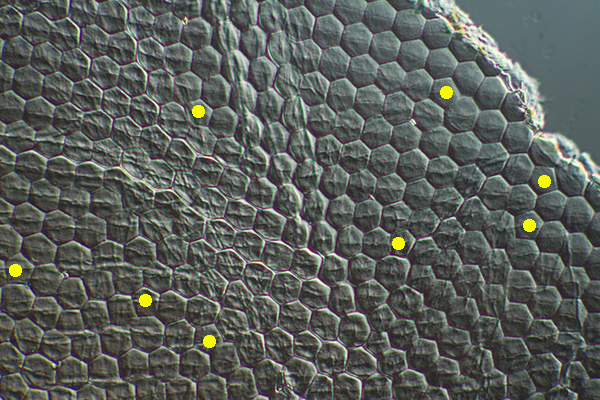
Above. Section of silk moth cleared cornea mounted in 50% glycerin in water, Photomicroscope, DIC with Zeiss 16/0.35 objective. A cleared flattened section of facets allows accurate measurement of their size e.g by measuring along a number and averaging. The facets shown are 25.6 µm between the parallel edges.
The author David Walker is an amateur microscopy enthusiast not a historian nor mathematician and welcomes any comments / corrections.
Acknowledgements:
With thanks to the members of the Mathematics Stack Exchange forum for providing answers to my query.
Published in the September 2015 edition of Micscape.
Please report any Web problems or offer general comments to the Micscape Editor .
Micscape is the on-line monthly magazine of the Microscopy UK web site at Microscopy-UK
© Onview.net
Ltd, Microscopy-UK, and all contributors 1995 onwards. All rights
reserved.
Main site is at www.microscopy-uk.org.uk
with full mirror at
www.microscopy-uk.net
.