In an earlier Micscape Lite article I shared my enthusiasm for the appeal of slide rules as collectibles and also for modern day use. Prior to the advent of affordable computing, whether mainframe / desktop computers or handheld calculators, slide rules in many forms were widely used in science, technology and engineering. I used one myself at high school in the mid 70s but by the late 70s, small electronic scientific calculators became widely available and cheap.

For many calculations, 3-4 significant figures provided by the typical 10 inch slide rule were more than adequate and it has been frequently noted that many engineering and technological feats of the late 19th and much of the first half of the 20th century were designed and built with the aid of the not so humble slide rule. But when greater precision and accuracy was required without the tedium of using extended log tables, the scales were lengthened in the typical model designs shown below.

These so-called long scale slide rules are often of particular interest to collectors partly because of their different design approaches, attractiveness as mathematical instruments and sometimes their sheer physical presence. In this article I show some of the different approaches used and is illustrated with examples from my own small collection.

A note on precision and accuracy
When considering the design and use of slide rules the important difference between precision and accuracy crops up. For a slide rule, its precision is how many significant digits a value can be read which is dependent on the tick mark frequency at that point on the scale which is in turn related to the scale length. The rule's accuracy is how the read-off value compares to the true value of a calculation and depends on how well the rule has been made and/or the scales have been divided. The user's skill in scale interpolation between tick marks is also a factor.

An illustration of the difference between precision and accuracy uses an example familiar to microscopists carrying out aquatic water sampling, the electronic pH meter. On the model I use the pH can be read to two decimal places on the LCD display, this is its precision (often called resolution in the model specs). However, unless the user is prepared to regularly calibrate the meter/pH probe whose properties can vary significantly e.g. with storage, its accuracy i.e its ability to read the true value of the solution's pH could vary widely.

A selection of slide rules from my collection which compares the size ranges of conventional linear slide rules with typical designs used to increase the scale length, some more compact than others! (For convenience all scale lengths are referred to the nearest inch, but many rules used 25 cm cf the 10 inch.)

Linear slide rules: 1 - 5" pocket slide rule (Jakar 33). 2 - 10" standard slide rule A W Faber 367 (Germany). 3 - 10" slide rule with doubled scales Faber 2/83N (Germany). 4 - 20" slide rule Nestler 0215 (Germany). Concentric circular scales: 6 - Gilson Binary (USA).

Spiral scale: 7 - Gilson Atlas type III (USA). Helical scale: 5 - Otis King calculator, type K (UK). 8 - Fuller calculator made by W F Stanley (UK).

The two rules 9 and 10 illustrate that to explore slide rule design and use doesn't need to cost very much. No. 9 is a very usable linear slide rule to download, print out and easy build, courtesy of Cliff Stoll's Scientific American article in 2006 'When Slide Rules Ruled'. No. 10 is my homemade Gilson spiral (as model 7 and just as accurate) courtesy of Wayne Harrison who wrote the script for the Gilson scales and using Ying Hum's clever design to use a DVD case as an accurate 'bearing' that doesn't wear.



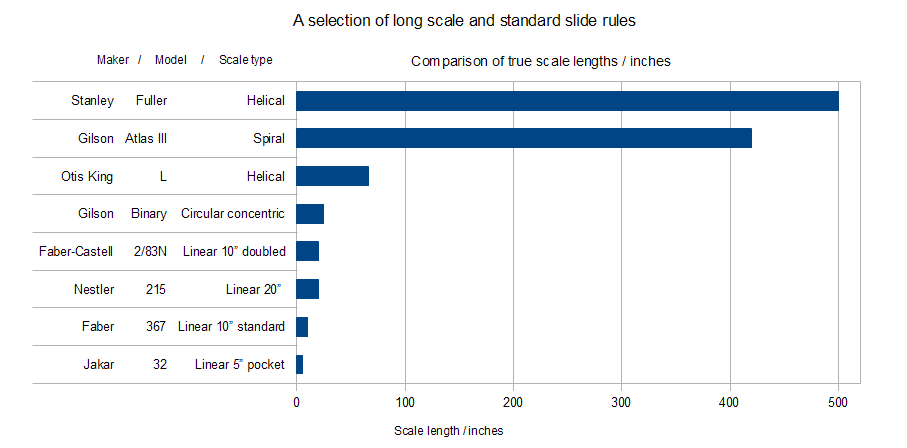
The graph above shows the actual scale lengths (from maker's specs) for the rules shown above and illustrates how different designs of rule can encompass different lengths of scale compared with their bulk. In actual use the 'effective scale length' i.e. how much better it is than a linear slide rule can be considerably greater depending on which part of a linear slide rule is used for comparison. See E J Chamberlain's paper in the references for an analysis and discussion of effective scale lengths.

A closer look at log scales—what are the benefits of longer scales?
On the scales of a ruler for linear measurement, the tick mark frequency remains the same but this is not the case with logarithmic scales required to exploit the principal of exponents to multiply and divide etc. A typical 25 cm slide rule at both ends of its scale is shown below. Longer logarithmic scales than the typical 25 cm (or 10 inch) would improve both the precision of the result read off and its accuracy at both ends of the scale.



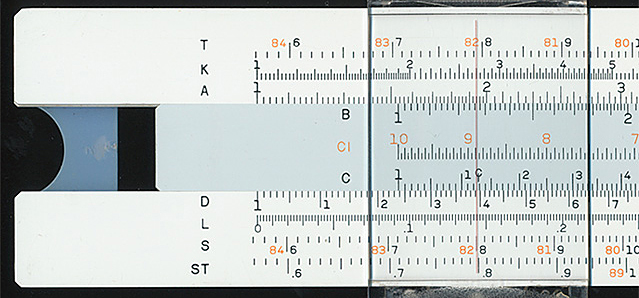
Above. A Hemmi P280 slide rule, a typical 10 inch / 25 cm model (the one I owned at high school in the 70s). At the lefthand end of the D scale, the tick mark frequency is 0.01 and with interpolation, four significant figures can be read at the cursor line with practice. At the far right, the tick frequency is 0.05 giving only three significant figures. Many calculations may demand more significant digits than such a slide rule can offer.

Two typical approaches by makers to offer longer scales was to either break down one or more scales into multiple parts on a 10 inch rule or by offering a longer rule. The former was the more practical—as the header image of the 20 inch (model no. 4 ) shows, the typical and widely available 20 inch rule with part extended slide was likely to poke a co-worker in the eye! However, with hands-on use it is very apparent that scales extended to 20 inches offered barely any improvement on the number of significant digits that could be read. Studies of long scale rules have shown (e.g by Edward J Chamberlain, see references) that the scale has to be approaching up to 10X longer to offer a unit increment in significant figures that could be read off cf the 10 inch rule.

Much longer scales were required, so what approaches did the makers offer?

The simple principle behind single scale 'slide rules'
For models that used greatly extended scales, many makers adopted a single log scale as the conventional slide rule design becomes increasingly impractical. Strictly speaking a mechanical calculator using a single logarithmic scale isn't a slide rule because there are not at least two sliding scales. Although some makers referred to their single scale models as a calculator and/or slide rule (e.g. Fuller). Single scale models are effectively a later variant of the original Gunter's scale but presented in a non-linear form (concentric, spiral, helical etc.). Edmund Gunter (Wikipedia entry) was the first to describe a single linear log scale for calculations using dividers to multiply and divide.

Although the long single scale models illustrated above by Gilson and Fuller can look rather daunting to use, the principle behind their use is more straightforward than a true slide rule and the use of a Gunter scale to demonstrate this is shown below.

Right. Upper image. The slide from a slide rule is shown, but only the lower single cycle log scale will be used—effectively a Gunter scale. A pair of dividers has been set to span 2 units. Lower image. The dividers are moved without adjusting its setting to start at 3. The divider multiplies by 2 to give 3 x 2 = 6 at the righthand pointer. (If the divider righthand pointer had been set to say 5, it would have divided by 2 to give 2.5 at the lefthand pointer.)

While using models such as the Fuller or the Gilson, it helps (as I do) to imagine their single log scale unwrapped to a line and that the two plastic cursors (on the Gilson) or the two brass pointers (on the Fuller) are equivalent to the divider points. After setting one variable with the cursors or pointers, the scale is moved relative to these fixed points to multiply or divide.

Fuller calculator with single helical scale
This is one of the most collectable long scale models and come up quite frequently on eBay. Prices vary widely but can sometimes slip through at well below their usual price—as my example did for the price of a very basic antique student microscope. It makes for an impressive display item, a conversational piece as well as instructive to use. It was in production for a long time indicating its success, from 1879 to ca. 1973 and this example was made by W F Stanley. They were date coded and my example was made in 1951. Later models such as this one had Bakelite formers and handle and still retains a trace of that typical phenolic odour.

The 500 inch scale is at the upper end of the long scale models offered and provided 5 significant figures near the lower index and almost 4 near the upper index. The penalty is bulk! The support on the box (see second image below) allowed regular use as it's unwieldy when handheld for long periods

Above. Close up of part of the Fuller calculator scale. Also showing the finely crafted brass fittings.

Above. A Fuller calculator in use in 1945 shown supported on its box.

In the image above, a Fuller calculator is in use by a lady at a firm making high quality optical instruments for the design calculations. The lady to her left may be using an Otis King calculator (no. 5 in header image). This film was produced in 1945—when the term 'computer' still often referred to the human resource. The commentary at this point notes that it can take up to a year to make the design calculations (ca. 2 min 10 secs into the 16 minute film). A discussion of this film in the Yahoo Microscope Forum suggests that it may be the Leicester factory of Taylor Hobson (with thanks to Mervyn Hobden).
Credits: © British Council Film Collection : Film title 'Let's See', released 1945, production company Merton Park Studios, director Robert Lapresle. Used under the British Council Creative Commons Licence with thanks. Thank you to Yahoo International Slide Group member 'weindan' for first spotting this film.

Gilson 8¼ inch diameter discs—comparing the concentric circle scales to a single spiral scale
Gilson were a US company that offered a range of rules on aluminium discs from the 1920s. The two examples below are 8¼ inches in diameter and compare and contrast the two scale types. These were widely used and both these models regularly sell on eBay for usually quite modest two figure sums. One of the appealing aspects of these designs is their appearance—attractive as mathematical instruments and tactile in use. The varnished scales usually survive well although the protruding cursors can be brittle and the rather complex pivot may need attention if stiffened.

Very high quality and accurate facsimiles can be readily made at little cost courtesy of hobbyists who have prepared scales for various rule designs, see model 10 in header image and the International Slide Rule Museum website which hosts a page of DIY designs from the simple linear to the sophisticated Thacher model.

Circular slide rules are not a new idea, some of the very earliest slide rules designs in the 17th century were scales on circular discs.

Above. Gilson Binary slide rule. This has concentric log scales so the longest scale is the outermost at 25 inches, so is comparable to a long scale linear rule but in a more compact physical form. An obvious disadvantage of this design is the lower precision / accuracy as the scales shorten towards the centre. The central pivot of this and the model below has a special clutch, the shorter cursor can move independently to the longer to set a value but the cursors move together retaining this value when the longer cursor is rotated. Thus allowing calculations to be made after setting the cursor separation.

Above. The Gilson Atlas type III slide rule using a single spiral scale of 420 inches. Although shorter than the Fuller's 500 inch helical scale it achieved almost the same accuracy. The Gilson is arguably the most effective long scale slide rule offering increased accuracy but with little bulk. For the collector it is also attractive and tactile in use.

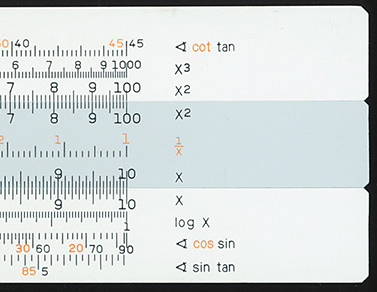
The benefit of the spiral over the concentric scale: Shown left above is the Gilson Binary outermost 'C' scale. The sub-divisions are 0.05 near '1', i.e. no better than a linear rule. On the right, the spiral scale of the Gilson Atlas has sub-divisions of 0.001 with interpolation between them possible to 0.0001. The Atlas allows almost five significant figure results to be read towards the beginning of the scale and above 4 at the far end. A further advantage of the spiral scale is that as the scale expands to the outer edge it gives a higher precision / accuracy cf. a linear scale at the end of the log cycle.

Above. The opposing side of both the Gilson Binary and Atlas had a set of trig scales using a single cursor. The 0 - 90 degrees was split over three concentric scales providing both greater precision and accuracy than linear slide rules with trig scales.

Appreciating the craftsmanship required to manufacture precise slide rules
As with other scientific collectables but once instruments in wide use, the devil is in the detail. All 10 - 20 inch slide rules for example adopt similar forms but close inspection sorts the finest makers and their craftsmanship from the also-rans. Before the wide availability of stable plastics, most slide rules were made from a variety of woods—typically with celluloid faces bonded on for the scales. The choice of woods, their treatment, stock and scale design and manufacture required a lot of care as very little warping, shrinkage etc would result in either an unusable or unreliable instrument.

This was particularly the case with the 20 inch linear rules to avoid distortion or binding of the double length stock / slide. A usable slide rule needs a careful balance between a tight fitting slide in the stock while free running along its length. Examples of two designs of 20 inch rule by two of the most well regarded makers are shown below.

Above. Left. Nestler model 0215 made from 1945+. This rule used mahogany with a second type of wood inserted to improve torsional strength (the paler layer marked with a yellow dot). This rule still sits perfectly flat after many decades.
Right: Faber-Castell 4/98 Elektro. Date stamp suggests 1952. This firm used both pearwood or high density laminate for this model depending on year of manufacture. I believe the heavy varnishing hides a high density wood laminate (seen more clearly with hand lens inspection of the end bevels). This model has metal strips inserted to improve strength, a common feature in many models. It has a pleasingly heavy feel in the hand cf the lighter Nestler, although my example has twisted somewhat with age but still works smoothly.

Above. The underside of both the above rules showing the attention to detail. Precision bonding of scale to wood, carefully bevelled and chamfered edges were all part of providing a precise instrument that felt good in the hand to use.

There are many parallels between collecting and using old mathematical instruments and older microscopes. They can both be enjoyed on many levels—exploring the history of the maker, the details of the model and how well it was made and works in use. An additional appeal of the slide rule is that it stretches the brain in exploring the versatility of their typical many scales. We tend to get lazy nowadays with a handheld calculator or smartphone with app giving results to a ridiculous number of decimal places in a split second. A slide rule makes you think of the calculation and requires the user to insert the decimal point. For many scientists and engineers before the electronic computer age, slide rules were an essential tool for their work.

A poster widely circulated on the Internet that makes a valid point. The originator's details seems to have got lost in the multiple sharings, so thanks to whoever you are and if a reader knows, please email me so that I can duly credit.

Comments to the author David Walker are welcomed.

Related Micscape articles
Slide rules, calculating aids, logarithms and related topics articles by David Walker in the 'Micscape Lite' section of the magazine.

Selected external resources for the slide rule enthusiast
United Kingdom Slide Rule Circle For UK and international members. Annual 'Gazette' with articles on a wide range of topics. Twice yearly 'Skid Stick' newsletter. Organises regular meetings.

The Oughtred Society US based with international membership. "Dedicated to the preservation and history of slide rules and other calculating instruments". This site has a wealth of its own resources, a tutorial of slide rule use and also access to older papers in its Journal. Its own links page is also carefully categorised and a good starting point for exploring the many resources online including online museums, sellers of new old stock and used slide rules. Organises regular meetings.

Rod Lovett's Slide Rules In addition to his own resources, he also offers a powerful search engine that can check for articles/papers in the major slide rule publications on any topic and also a search engine for checking prices that models sold for at auction.

Edwin J. Chamberlain has carefully researched long scale rules and has written extensively on them. Many of these papers can be accessed via Rod Lovett's slide rule literature database. Of particular note and of value when assessing my own examples of long scale rules is his paper 'Long Scale Slide Rules', J. Oughtred Society, vol. 8, no. 1, Spring, 1994, 24-34. This paper includes a quantitative assessment of the significant figures that can be read for a wide range of models.

Slide rule, precision, accuracy and significant digits A page on Dave Hoyer's website with a particularly clear explanation of how these parameters apply to slide rules. His own selection of commercial rules presented includes a homemade 'Eximius Diu 6' built as a quest to build a spiral scale slide rule with the world's longest scale, available to download and print out.

Microscopy UK Front Page
Micscape Magazine
Article Library

---

© Microscopy UK or their contributors.

Published in the May 2015 edition of Micscape.

Please report any Web problems or offer general comments to the Micscape Editor .

Micscape is the on-line monthly magazine of the Microscopy UK web site at Microscopy-UK

---

© Onview.net Ltd, Microscopy-UK, and all contributors 1995 onwards. All rights reserved.
Main site is at www.microscopy-uk.org.uk with full mirror at www.microscopy-uk.net .