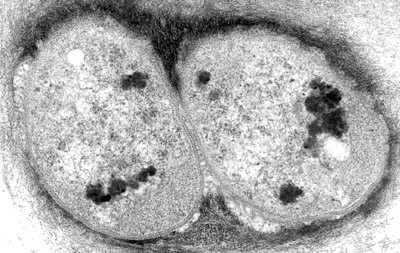
Completion of bacterial division, TEM mag. 20 000x, from
the author's 'Speaking of Cells' Micscape article.
|
About Magnification and Resolution M. Halit UMAR, MD., PhD. |
These two words, 'Magnification' and 'Resolution' are well-known terms for microscopists and morphologists. Who doesn't know a magnifying glass? A skillfully manufactured glass makes it possible to see some details, which are not easily visible to a naked eye, by magnifying the object to be studied or read. How a piece of glass results in magnification was studied by scientists centuries ago and explained by physical laws. For the human eye, seeing objects, in more and more detail, depends on light. No light means no seeing! The human eye is a marvelous but, at the same time, a restricted organ. My cat can easily find her way in the dark when I cannot see anything in the very same place. For intelligent (human) beings such restrictions are known but not insurmountable. If we cannot see fine details, we can just magnify a subject through a glass or by a microscope or something like that. The art of making visible is, in reality, a large domain of the applied sciences of which a microscopist makes thankfully use.
And, then, some justifiable questions comes to our mind: How much can we magnify? Even this expression reveals the unspoken acceptance of a possible limit of the magnification process. And it is true, we cannot magnify things endlessly to see more details without compromising or losing information. There must be an equation describing this, and there is, of course, a mathematical outcome for it. We may express such an equilibrium with a scientific term. i.e., the resolution.
A microscopist knows that he/she can achieve a maximum of magnification with the light microscope which is about 1000x.
Intelligent minds solved this limitation by
using electron bundles instead of visible light. So, this ingenious technique
opened a new era for morphologists making it possible to see more and more with an
extreme power of resolution which may be expressed by the distance between two
visible points to human eye. Nowadays, the distance of a few nanometers is achievable
and indeed
on a molecular scale, and we can see details using such high power magnifications.

Completion
of bacterial division, TEM mag. 20 000x, from
the author's 'Speaking
of Cells' Micscape article.
Since the resolution is a mathematical equation, it would be clear that we gain something at the expense of something else. Let me explain this fact with the aid of a puzzle. If a puzzle consists of 100 pieces, looking at some of the pieces of the puzzle you may readily guess what the whole image is. If it consists of 1000 pieces, it would be rather difficult to find out what the whole image could be. And, what about if it consists of 1 000 000 pieces and you look at a few of them to decipher the whole image? The human mind loses its analytical power at high resolution. I really wonder how Einstein or Marie Curie or Galileo Galilei, or Isaac Newton would react upon this last example of puzzle consisting of billions of pieces.

Madrid Botanical Garden, Science Exposition: De Einstein al Futuro.

At the same exposition hall, the original book of Isaac Newton:
Philosophiae Naturalis PRINCIPIA Mathematica.
You can also experiment using your PC screen to see what you gain or loose by high resolution. Just type letter A and magnify it:

Accept each pixel as one piece of a puzzle. Take a few of the pieces (pixels) and, on the basis of these pixels, try to decipher the whole image. Well, what is your outcome? Could you say that these pieces are a letter A? Can you see what are you going to lose with a higher resolution?
During my recent visit to Madrid Botanical Garden, while admiring beautiful trees and plants, I find so many objects to reflect on the levels of magnification and resolution, from astronomical to molecular structures. In our world, with or without visible morphological units and organisms, we can find an immense source of philosophical and scientific subjects.

A tree, Platanus sp. one of the thousands of the trees at the Madrid Botanical Garden.
Comments to the author are welcomed. M. H. UMAR, MD PhD
Please report any Web problems or offer general comments to the Micscape Editor.
Micscape is the on-line monthly magazine of the Microscopy UK website at Microscopy-UK